Need a One Sample t-Test and Variance Test in Excel?
QI Macros can do it for you!
Create one-sample t-tests and variance tests
using
QI Macros:
- Select your data.
- Click on QI Macros menu > Statistical Tools > F & t Tests > One-Sample t-Test
- QI Macros will do the math and analysis for you.
Go Deeper: >A one sample t-Test compares test data to a specific value. It helps determine if the sample is greater than, less than or equal to the value.
Note: Excel does NOT do one-sample t-tests; QI Macros adds this functionality.
One Sample t-Test Example
QI Macros adds a new tab to Excel's menu. To conduct a t-Test using QI Macros follow these steps:
Let's say you want to know if the life of a light bulb is greater than 2,500 hours. Take your sample and input the data in Excel.
- Click and drag over the data to select it.
- Next, click on the QI Macros Menu > Statistical Tools > F & t Tests, and then select "t-Test: one sample":
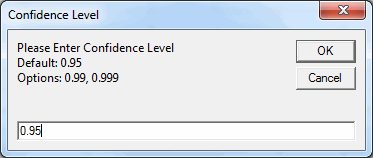
- QI Macros will prompt for a confidence level (default = 0.95)
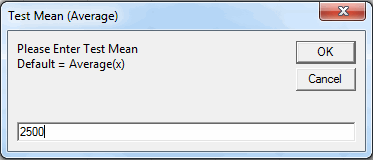
and a Test Mean (light bulb life is less than or equal to 2,500 hours)
QI Macros will perform the calculations and interpret the results for you:
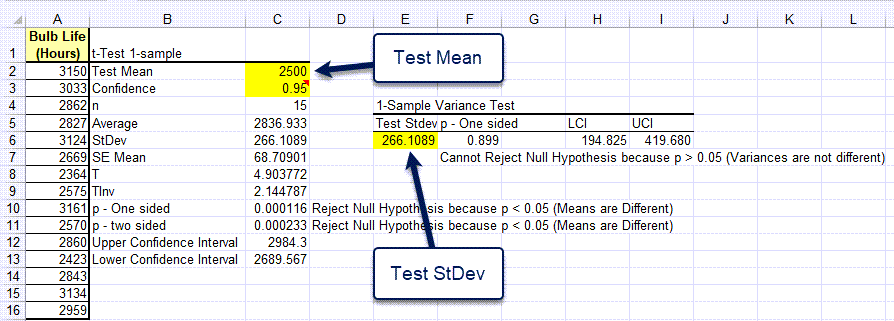
In this example, p-value = 0.00016 and alpha = 0.05 (1 - .95 the confidence level). Since p < .05 we "Reject the Null Hypothesis" (Means are Different/Means are not the Same). You can also change the test mean and the calculations with change.
One Sample Variance Test
To test the variance, put the standard deviation (Stdev) test value in cell E6. The p-value will calculate in F6.
Note: TInv means "T Inverse" and is used in calculating the upper and lower confidence intervals.
What's Cool about QI Macros Statistical Add-in for Excel?
Interprets the Results for You: QI Macros compares the p value to alpha and tells you what that means. In the above example, QI Macros tells you to "Reject the Null Hypothesis," because p < 0.05 (Means are Different/Means are not the Same).
Interactive Results: QI Macros lets you change the confidence level and test mean to see what impact those changes have on your results. See areas outlined in red for cells that can be changed.
Interpreting the t-Test One-Sample Results Manually
So we develop a null hypothesis (H0) that light bulb life is less than or equal to 2,500 hours and the alternate hypothesis (Ha) that bulb life is greater than 2,500 hours:
- H0 <= 2,500 hours
- Ha > 2,500 hours
Now, conduct a test of light bulb life and enter the data into Excel.
QI Macros automatically interprets the results for you. However, here is some guidance if you want to do that yourself.
Since the null hypothesis is that bulb life is less than or equal to 2,500, this is a one-sided test. Therefore, use the one-tail values for your analysis:
If |
Then |
| t-Test statistic > critical value (i.e. t > tcrit) |
Reject the null hypothesis |
| t-Test statistic < critical value (i.e. t < tcrit) |
Cannot Reject the null hypothesis/Accept the null hypothesis |
| p value < a | Reject the null hypothesis |
| p value > a | Cannot Reject the null hypothesis/Accept the null hypothesis |
Note: The two-sided values would apply if our null hypothesis was that:
H0: mean = 2,500 hours
Since the t statistic > t critical (4.904 > 1.76131) and p value < a (0.000116 < 0.05), we can reject the null hypothesis that bulb life is less than or equal to 2,500.
We can say that we are 95% confident that the bulb life is greater than 2,500 hours.
Customer Service - Another t-Test One Sample Example
Let's say you want to know if wait times in a branch bank are not greater than three minutes at a 95% confidence level. Mystery shoppers routinely visit the branch and collect their wait time. This gives us the data we need to test the hypothesis.
Select your data and then "t-Test: one-sample" from QI Macros > F & t Tests:
Answer the prompts: Confidence level .95 and test mean 3.
- H0 <= 3 minutes
- Ha > 3 minutes
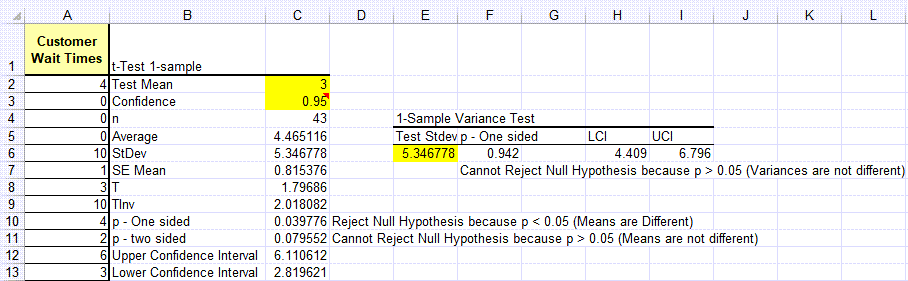
The one-sided p value < a (.039776 is less than 0.05 (1-0.95)), so we must "Reject the Null Hypothesis" that bank wait times are less than or equal to 3 minutes.
We can say that we are 95% confident that wait times are greater than 3 minutes.
Stop Struggling with One-Sample t-Tests!
Start creating your One-Sample t-Tests in just minutes.
Download a free 30-day trial. Get One-Sample t-Tests now!
Why Choose QI Macros Statistical Software for Excel?
Easy to Use
- Works Right in Excel
- Interprets p-values for You
- Accurate No-Worry Results
- Free Training Anytime
Proven and Trusted
- 100,000 Users in 80 Countries
- Celebrating 20th Anniversary
- Five Star CNET Rating - Virus Free
Affordable
- Only $349 USD
Quantity Discounts Available - No annual fees
- Free Technical Support
