Looking for a Sample Size Calculator in Excel?
QI Macros Ready-Made Template Will Calculate Sample Size for You!
QI Macros Sample Size Calculator works with both variable (measured) and attribute (counted) data.
Calculate Sample Size using QI Macros
- Click on QI Macros menu > Find QI Macros Tools > Sample
- QI Macros will pull up the Sample Size Template for you.
- Adjust yellow shaded cells to get the sample size.
How to Calculate Sample Size using QI Macros template
QI Macros adds a new tab to your Excel menu. To open the sample size template just click on QI Macros menu > Calculators > Sample Size Calculator. You should see the following:

To calculate a sample size you need to know:
- The confidence level required (90%, 95%, 99%)
α = 0.1, 0.05, 0.01 (Type I Error) - The Power required (80%, 85%, 90%)
β = 0.2, 0.15, 0.1 (Type II Error) - The desired width of the confidence interval
δ - Maximum allowable error of the estimate
= 1/2 * tolerance - σ - estimated standard deviation (high value - low value)/6.
To prevent calculation problems, QI Macros uses a default value = 0.167 (1/6).
The defaults are set to standard parameters, but can be changed.
Confidence Level
In sampling, you want to know how well a sample reflects the total population. The α = 0.05 - 95% confidence level means you can be 95% certain that the sample reflects the population within the confidence interval.
Step 1 - Choose alpha α = 0.05 - 95% Confidence Level
Step 2 - Choose beta β =
0.1 - 90% Power
Confidence Interval
The confidence interval represents the range of values which includes the true value of the population parameter being measured.
Step 3 - Set the confidence interval to half the tolerance or maximum allowable error of the estimate. (e.g., + 0.05, 2, etc.)
Step 4 - Attribute data (pass/fail, etc.) - Set percent defects to 0.5
If 95 out of 100 are good and only 5 are bad, then you wouldn't need a very large sample to estimate the population. If 50 are bad and 50 are good, you'd need a much larger sample to achieve the desired confidence level. Since you don't know beforehand how many are good or bad, you can set the attribute field to (50% or 0.5).
Step 5 - Variable Data - Enter Standard Deviation
If you know the standard deviation of your data (from past studies), then you can use the standard deviation.
If you know the specification tolerance, then you can use (maximum value - minimum value)/6 as your standard deviation. (The default is 1/6 = 0.167).
Step 6 - Enter the total population (if known)
Using the default values (95%, + 0.05, Stdev = 0.167)
Step 7- Read the Sample Size
Use the sample size calculated for your type of data: Attribute or Variable.

Variable Sample Size: If we are using variable data and just α the sample size would be 43.
Using α and β the sample size would be 118.
***
Please Note: Our Sampling Tables are identical to that of the ANSI Z1.4 tables. QI Macros offers general inspection levels, however not special inspection levels.
Attribute Sample Size Calculator Example
Attribute Sample Size: What if you were using attribute data, (e.g., counting the number of defective coins in a vat at the Denver Mint) but didn't know how many coins were in the vat? You'd need 384 coins to be 95% confident that the coins fell within the 5% interval.
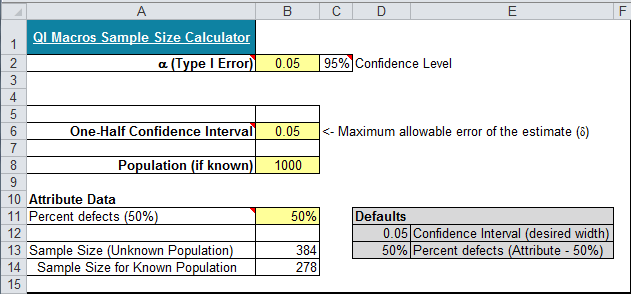
What if you knew there were 1000 coins in the vat (population known)? You only need 278 to be confident.
What if you changed the confidence interval to be + 0.1?
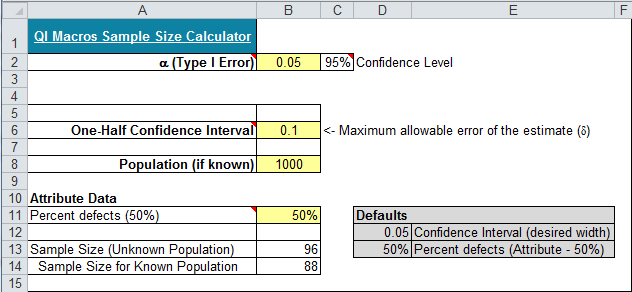
You only need 88 to be 95% confident.
Variable Sample Size Calculator Example
A sample must be selected to estimate the mean length of a part in a population. Almost all production falls between 2.009 and 2.027 inches.
Estimated standard deviation = (2.027 - 2.009) / 6 = 0.003.
And you want to be 95% confident that the sample is within +/- 0.001 of the true mean. Enter the data as shown below:
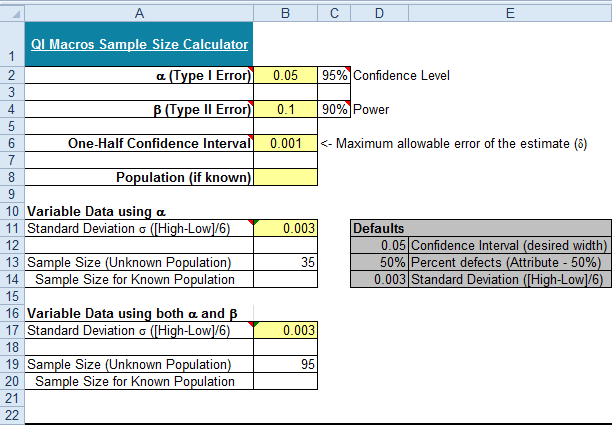
You need 35 samples using α alone and 95 using α and β together.
Haven't you waited long enough?
Start creating your Sample Size Calculator in just minutes.
Download a free 30-day trial. Get the Sample Size Calculator now!
The Sample Size Calculator is one of many tools included in QI Macros add-in for Excel.
QI Macros adds a new tab to Excel's menu, making it easy to find any tool you need. If you can't locate a tool, use the find tools feature on the far right side of QI Macros menu.


