Design of Experiments Case Study
Two-factors at three levels can be handled using ANOVA
A school wants to increase attendance at business seminars. The administrator has attendance data from two sets of seminars held on Mon./Wed./Fri. in 1-2-4 hour lengths:
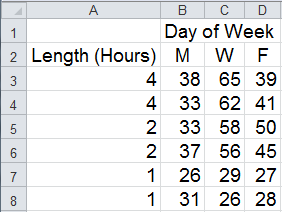
Which combination of seminar days/times will give the best attendance?
ANOVA Two-Factor with Replication
With the QI Macros, select the data and run ANOVA Two-Factor with (2) replications:
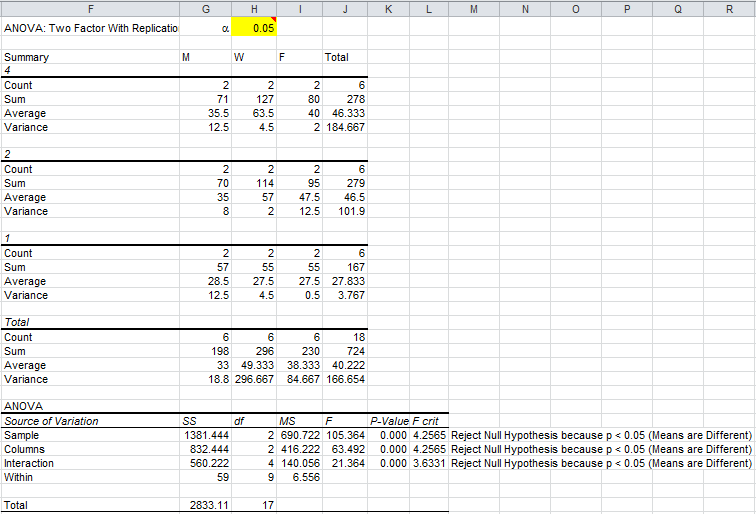
From the p-values, we can see that length, day and interaction affect attendance. If we plot the averages for each length by day we can see that longer Wednesday seminars work best:
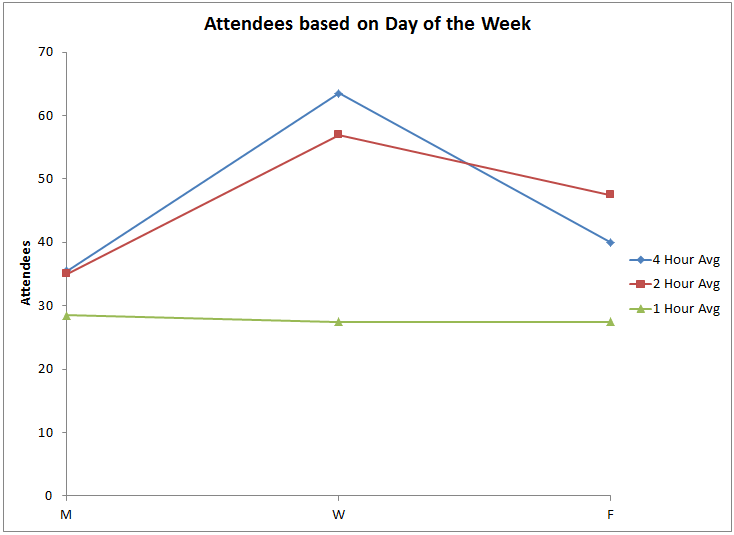
Mondays and one-hour seminars simply don't generate the attendance. Two or four hour seminars on Wednesday attract the most attendees. Friday two-hour seminars might also be an option.
Note: You can perform as many replications as you would like to, as long as you have the same number of rows for each "Length (Hours)". For instance, if you setup your data w/ 4 rows of 4 Hours, you would also need to have 4 rows of 2 Hours and 4 rows of 1 Hour.
What if there were no replications:
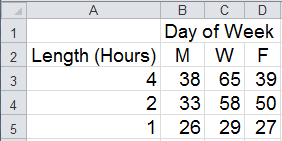
ANOVA Two-Factor without Replication would give:
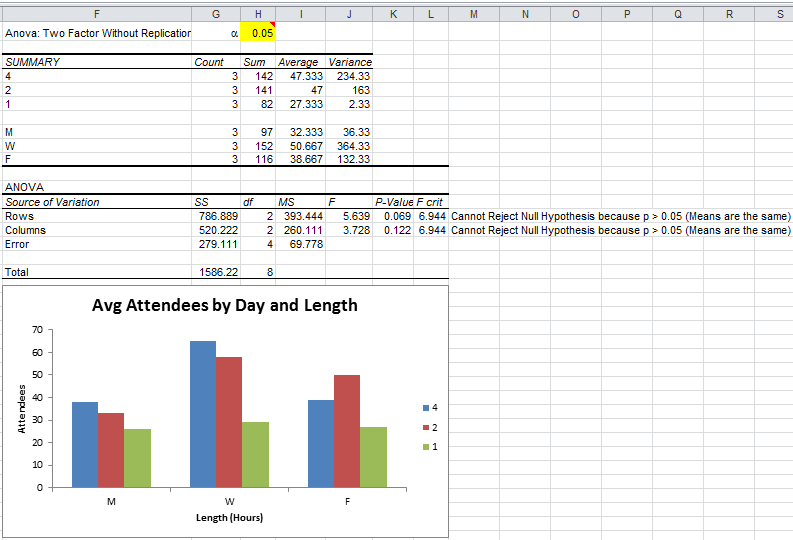
In this case, p-value of 0.069 is slightly larger than alpha=0.05, so we can't confirm that different days and times are statistically significant. A graph of the data does suggest, however, that Wed, 2-4 hour seminars attract the most attendance:
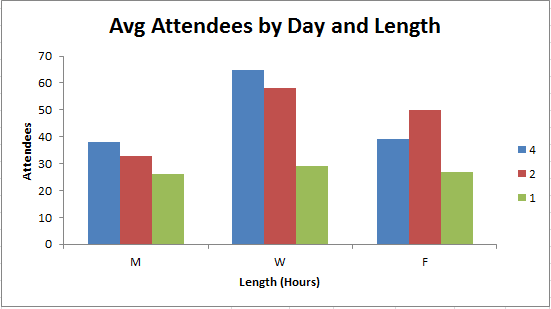
So, there's a little taste of 32 factor DOE using ANOVA with the QI Macros.

